Página principal
Estás en:
![]()
Otros temas de
esta sección:
Objetivos,
propósitos y
expectativas
de logro.
El
niño de 1 año
El
niño de 2 años
El
niño de 5 años
Características
evolutivas,
3 a 5 años

Salud
y
prevención de
accidentes
_________________
La génesis del pensamiento matemático:
Pensar y "jugar" la matemática
El pensamiento matemático está presente en la vida cotidiana del niño desde muy temprana edad, porque forma parte de la cultura que lo rodea y de la cual forma parte. Existen nociones de tiempo y espacio, agrupamiento, movimiento y juego que permiten desarrollar nociones previas, necesarias para la adquisición del número.
¿Cómo se genera el pensamiento matemático?
La visión constructivista del aprendizaje de la matemática tiene como teoría de base el trabajo de Jean Piaget, especialmente, la descripción sobre la génesis del número. De acuerdo a esta teoría, los conceptos matemáticos primarios se construyen mediante la abstracción reflexiva. El sujeto realiza una lectura de sus propias acciones sobre los objetos, lo que le permite descubrir relaciones entre ellas y luego reflejarlas en la realidad exterior. Por tanto, el desarrollo de la competencia numérica del niño se halla relacionada con el desarrollo de las nociones lógico-matemáticas.
Desde muy temprana edad, los niños van adquiriendo una cantidad de conocimientos y estrategias para abordar sus necesidades y responder a sus inquietudes e intereses. Éstos aún son informales (aprendidos fuera de la escuela), pero les permiten lograr resolver situaciones que conllevan las operaciones aritméticas básicas (suma, resta, multiplicación y división).
Desde estos primeros esquemas propios de acción, se generan nuevos esquemas que complementan y amplían los anteriores, hasta llegar a transformarse en "pensamiento".
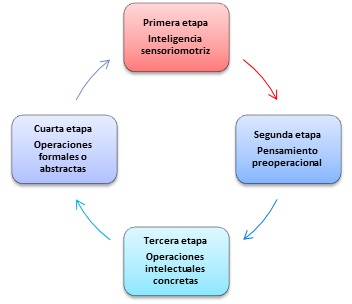
En sus estudios sobre Psicología Genética, Piaget concluyó en que todos los niños evolucionan en una secuencia ordenada. Estas etapas, que llamó "estadios", son: La inteligencia sensorio-motriz, el pensamiento pre-operacional, las operaciones intelectuales concretas y las operaciones formales o abstractas.
Piaget interpreta que todos los niños evolucionan a través de esta secuencia ordenada de estadios. La interpretación que realizan los sujetos sobre el mundo es cualitativamente distinta dentro de cada período, alcanzando su nivel máximo en la adolescencia y en la etapa adulta. Así, el conocimiento del mundo que posee el niño cambia cuando lo hace la estructura cognitiva que soporta dicha información. Es decir, el conocimiento no supone un fiel reflejo de la realidad hasta que el sujeto alcance el pensamiento formal.
El niño va comprendiendo progresivamente el mundo que lo rodea del siguiente modo:
a) Mejorando su sensibilidad a las contradicciones.
b) Realizando operaciones mentales
c) Comprendiendo las transformaciones
d) Adquiriendo la noción de número.Asimilación- Acomodación:
"Cuando un individuo se enfrenta a una situación, en particular a un problema matemático, intenta asimilar dicha situación a esquemas cognitivos existentes. Es decir, intentar resolver tal problema mediante los conocimientos que ya posee y que se sitúan en esquemas conceptuales existentes. Como resultado de la asimilación, el esquema cognitivo existente se reconstruye o expande para acomodar la situación".(1)
Esta relación de asimilación- acomodación producirá el aprendizaje significativo.Las nociones temporales y espaciales
Previamente a la noción de número, el niño adquiere las primeras nociones de espacio y tiempo. En su artículo "Espacio y tiempo en la educación infantil", María Isabel Rael Fuster (2) señala que el tiempo constituye un todo indisociable con el espacio ya que el primero se percibe por el movimiento y el movimiento necesita un espacio. Antes de los seis años, hay una subordinación del tiempo al espacio por parte del niño; posteriormente éste será capaz de diferenciar ambos.
¿Por qué son tan importantes?
Las nociones espacio- temporales son de gran importancia en el proceso de aprendizaje, ya que contribuyen principalmente a la adquisición de las competencias de conocimiento e interacción con el mundo físico, social y ciudadano , y a la capacidad de "aprender a aprender". Serán un requisito para los aprendizajes matemáticos, plásticos, musicales, de lectoescritura, de conocimiento del medio, la prevención de accidentes, y para adquirir hábitos de orden, trabajo y convivencia.
Según Piaget, la evolución del espacio en el niño, la definen los siguientes niveles: un espacio topológico, un espacio proyectivo, un espacio euclidiano y un espacio racional. Estos niveles proporcionan tipos de información espacial que incluyen:
Orientación - Dimensión - Tamaño - Dirección - Formas.
El espacio se vivencia a través del movimiento del propio cuerpo (succionar, asir, gatear, caminar), de los objetos (caen, ruedan, vienen, van), de las acciones (tirar, subir, bajar, arriba-abajo, adelante-atrás, adentro-afuera). Se representa por medio de construcciones, dibujo y modelado. Esta representación requiere de la motricidad fina y coordinación óculo-manual.
Para escribir los números, es necesario el desarrollo paralelo de estas habilidades. Sus falencias implican dificultades en este aprendizaje; de ahí la importancia de conocerlas y poder trabajarlas.Etapas en la construcción del número
El número es concebido por Piaget como la fusión de las clases (términos individuales, constituida por su propia extensión) y de las relaciones (lo que permite reunir los términos según su equivalencia u orden; constituida por la propia comprensión); las primeras proporcionan el aspecto cardinal del número y las segundas el aspecto ordinal. Esto es así porque en el concepto de "clase" se alcanza un equilibrio entre comprensión y extensión (la comprensión se refiere a la cualidad que poseen todos los individuos que pertenecen a la misma clase).
Las etapas en la construcción del número conservan cierta forma similar con las de la constitución de las clasificaciones y de las seriaciones.- En una primera etapa, se observa la ausencia de la conservación del número porque el niño confunde la cantidad numérica (número de elementos) con la longitud espacial (disposición o ubicación espacial de los elementos del conjunto). Hay aún, una confusión entre los aspectos lógicos e infralógicos.
- En una segunda etapa el niño, si bien puede efectuar correspondencia término a término entre los elementos de dos conjuntos, niega la conservación de la cantidad, cuando se cambia la disposición espacial de los elementos de uno de los conjuntos, porque este cambio da como resultado una configuración perceptiva distinta a la anterior. Los estados (los dos subconjuntos) que se ponen ahora en correspondencia han dejado de ser idénticos desde el punto de vista perceptivo; sólo su identidad puede ser entendida como tal si se abstrae el resultado de las acciones que generaron transformaciones espaciales, y se consideran los elementos discontinuos como unidades desprovistas de toda cualidad y de toda relación espacial.
- Finalmente, la tercera etapa es la de la conservación del número más allá de toda configuración perceptiva, es decir, más allá de toda disposición espacial.El juego didáctico en el aprendizaje
El juego constituye una natural descarga del exceso de energía que posee el niño por sus propias características. Para nadie es desconocido que la mayor parte de la vida del niño la dedica al juego, a través del cual canalizan sus energías, sus ansiedades, sus miedos, y desarrolla su curiosidad y creatividad; por ello se suele afirmar que el jugar es la esencia del niño, además se puede decir que no existe mejor ejercicio para el niño que el juego, convirtiéndose en una verdadera gimnasia que beneficia todas las dimensiones del desarrollo.
¿Cuáles son las actividades que favorecen el pensamiento matemático?
Si se observa a un niño jugar y se registran las estrategias que pone en juego durante la partida, de seguro se obtendrá una larga lista de razonamientos lógico-matemáticos. El juego es un recurso irreemplazable en la enseñanza, su función didáctica enriquece todo tipo de aprendizaje: social, emocional, cognitivo, mediante recursos atrayentes y divertidos como: puzzles, rompecabezas, adivinanzas, juegos de mesa, naipes, dados, juego del "quién es quién", etc.
El juego infantil es entonces un medio de aprendizaje espontáneo y de ejercitación de competencias intelectuales, físicas, sociales y morales. Para plantear propuestas en el aula, es necesario saber la evolución del juego infantil. Se toma la propuesta de Piaget:
- Juego de simple ejercicio o sensorio motor, hasta los 4 años. Es juego funcional hasta los 6 meses, juego de exploración de 6 a 12 meses y juego de autoafirmación de 1 a 2 años.
- Juego simbólico, de 2 a 12 años. De imitación, de 2 a 4, de escenificación primaria, de 4 a 7, y de escenificación secundaria, de 7 a 12 años.
- Juego de reglas, de 6/ 8 años en adelante.
- Juego de construcción y destrucción, no responde a ninguna sucesión de otro juego sino que se desarrolla a partir del juego simbólico.
Referencias y bibliografía:
- (1) IBAÑEZ IZQUIERDO, Leonor-PONCE RAMOS, Alicia. "El aprendizaje de las matemáticas según las etapas o estadios de Piaget".
- - (2) Espacio y tiempo en la educación infantil - http://www.csi-csif.es/andalucia/modules/mod_ense/revista/pdf/Numero_15/ISABEL_RAEL_1.pdf
- - RADRIZZANI GOÑI, A.M.-GONZÁLEZ, A. El niño y el juego.2.Las operaciones lógico matemáticas y el juego reglado. 1994 (p.46)
 Búsqueda personalizada
Búsqueda personalizada